
Assistant professor
sylvain.prolhac(at)irsamc.ups-tlse.fr
+33 (0)5 61 55 65 82
Building 3R1B4, office 324 (3rd floor)
Address : Laboratoire de Physique Théorique,
Université de Toulouse, 118 Route de Narbonne,
31062 Toulouse Cedex 4, France
Master 2 internship proposal
PhD thesis proposal
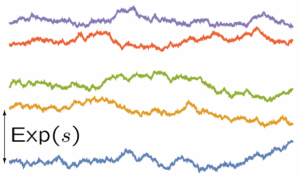
I have been working on a one-dimensional non-equilibrium universality class known as KPZ, which describes the fluctuations of some growing interfaces as well as classical and quantum fluids.
I am especially interested in finite volume effects, corresponding to a regime where the correlation length of the fluctuations is of the same order of magnitude as the size of the system. The temporal evolution of the system then describes the full relaxation process to stationarity, starting from a given initial state.
In particular, I showed recently that KPZ fluctuations in finite volume describe the relaxation to stationarity for some integrable spin chains :
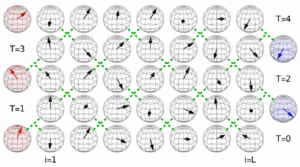
On the technical side, KPZ fluctuations in finite volume can be obtained by taking the large scale limit of interacting particle systems such as the totally asymmetric simple exclusion process (TASEP) :
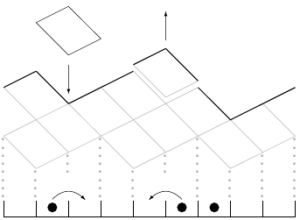
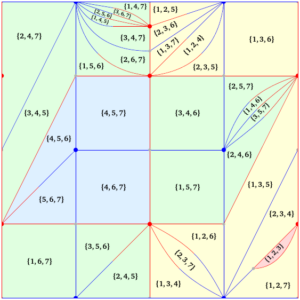
Selected papers (full list on arXiv):
Review paper, based on my habilitation thesis :
Exact formulas for KPZ fluctuations in finite volume
Application to integrable spin chains
Non-intersecting Brownian processes
Riemann surfaces
Multiple species of particles
Spectral gaps