PROLHAC Sylvain

Address : Laboratoire de Physique Théorique,
Université de Toulouse, 118 Route de Narbonne,
31062 Toulouse Cedex 4, France

Master 2 internship proposal
PhD thesis proposal

I have been working on a one-dimensional non-equilibrium universality class known as KPZ, which describes the fluctuations of some growing interfaces as well as classical and quantum fluids.

I am especially interested in finite volume effects, corresponding to a regime where the correlation length of the fluctuations is of the same order of magnitude as the size of the system. The temporal evolution of the system then describes the full relaxation process to stationarity, starting from a given initial state.

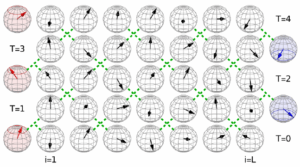
In particular, I showed recently that KPZ fluctuations in finite volume describe the relaxation to stationarity for some integrable spin chains :

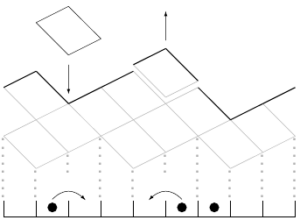
On the technical side, KPZ fluctuations in finite volume can be obtained by taking the large scale limit of interacting particle systems such as the totally asymmetric simple exclusion process (TASEP) :

 

Exact formulas then involve contour integrals on Riemann surfaces, whose genus tends to infinity in the KPZ scaling limit :

Additionally, stationary KPZ fluctuations have a simple representation in terms of non-intersecting Brownian processes :

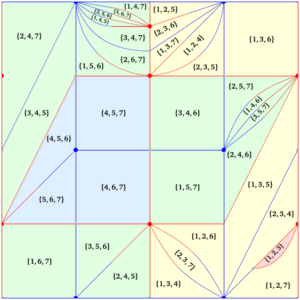
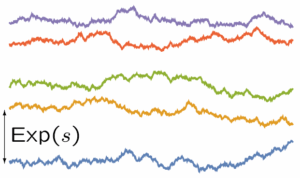
Selected papers (full list on arXiv):

Review paper, based on my habilitation thesis :

• S.Prolhac, KPZ fluctuations in finite volume, SciPost Phys. Lect. Notes 81 (2024) (arXiv:2401.15016)

Exact formulas for KPZ fluctuations in finite volume

• S. Prolhac, Finite-time fluctuations for the totally asymmetric exclusion process, Phys. Rev. Lett. 116 (2016) 090601 (arXiv:1511.04064)

Application to integrable spin chains

• S. Prolhac, Cheaper access to universal fluctuations in integrable spin chains from boundary effects (2025) (arXiv:2509.05176)

Non-intersecting Brownian processes

• S. Prolhac and K. Mallick, Brownian bridges for late time asymptotics of KPZ fluctuations in finite volume, J. Stat. Phys. 173 (2018) 322-361 (arXiv:1805.03187)
• S. Prolhac, Approach to stationarity for the KPZ fixed point with boundaries, EPL148 11002 (2024) (arXiv:2407.07012)

Riemann surfaces

• S. Prolhac, Riemann surfaces for KPZ with periodic boundaries, SciPost Phys. 8, 008 (2020) (arXiv:1908.08907)
• S. Prolhac, Riemann surface for TASEP with periodic boundaries, J. Phys. A: Math. Theor. 53 445003 (2020) (arXiv:2006.15096)
• S. Prolhac, Probability of a single current, J. Stat. Phys. 191 133 (2024) (arXiv:2308.11693)

Multiple species of particles

• S. Prolhac, M. R. Evans and K. Mallick, Matrix product solution of the multispecies partially asymmetric exclusion process, J. Phys. A: Math. Theor. 42 165004 (2009) (arXiv:0812.3293)
• S. Prolhac, Current fluctuations for the second class particle : joint statistics, J. Phys. A: Math. Theor. 58 325004 (2025) (arXiv:2503.10531)

Spectral gaps

• S. Prolhac, Perturbative solution for the spectral gap of the weakly asymmetric exclusion process, J. Phys. A: Math. Theor. (2017) 50:315001 (arXiv:1703.04596)
• U. Godreau and S. Prolhac, Spectral gaps of open TASEP in the maximal current phase, J. Phys. A: Math. Theor. (2020) 53 385006 (arXiv:2005.04461)