How does the low-temperature free energy of one-dimensional interacting quantum liquids behaves beyond the standard temperature-squared correction, a well-known result from conformal field theory? A recent study of Zoran Ristivojevic of the Laboratory of Theoretical Physics in Toulouse and his collaborator Miłosz Panfil from the University of Warsaw published in Physical Review Letters, addresses this question.
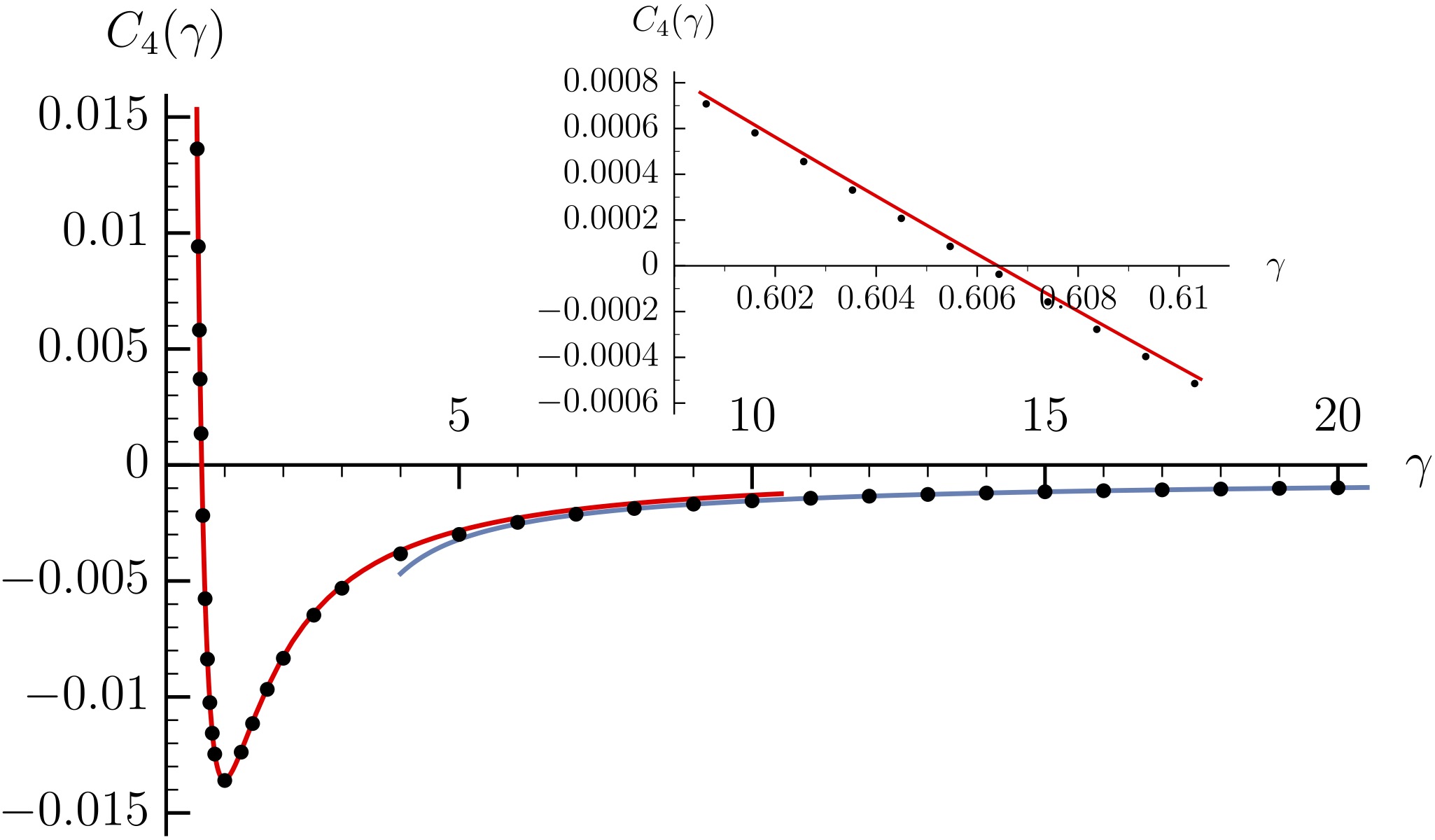
Quantum integrable gases are distinguished by the presence of stable quasiparticles, whose distribution governs the thermodynamic properties of the system. In the Lieb-Liniger model, describing the one-dimensional bosons with contact interaction, at zero temperature, this distribution resembles a Fermi sea possessing a non-zero curvature near the Fermi edges that carries the particularities of the model. In the published work, the exact, non-perturbative relations between the curvature and the thermodynamics of the gas at low temperatures are established, enabling the calculation of the first nontrivial temperature correction. It scales with the fourth power of the temperature. As a result, the heat capacity acquires the curvature. Interestingly, the curvature vanishes at a particular value of the interaction strength, marking the crossover from concave to convex behavior. The obtained results are experimentally accessible, as the quasi-particle distribution can be directly probed in cold atom setups, and could be useful for future precision measurements in quantum gases.
Reference: Miłosz Panfil and Zoran Ristivojevic, Local Properties of the Rapidity Distribution in the Lieb-Liniger Model, Phys. Rev. Lett. 135, 020408 (2025).