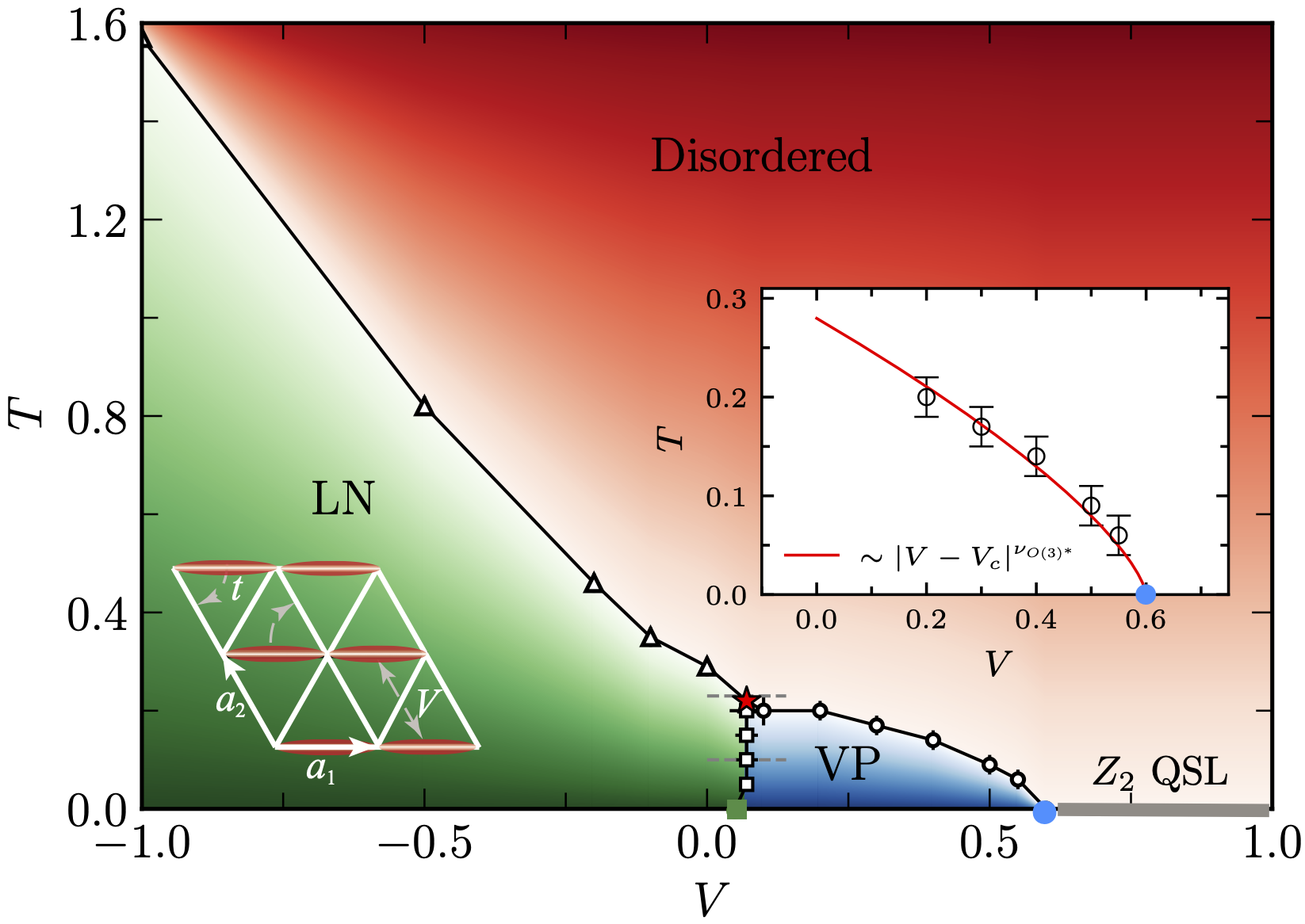
The quantum loop and dimer models are archetypal correlated systems with local constraints. With natural foundations in statistical mechanics, they are of direct relevance to various important physical concepts and systems, such as topological order, lattice gauge theories, geometric frustrations, or more recently Rydberg array quantum simulators. However, how the thermal fluctuations interact with constraints has not been explored in the important class of nonbipartite geometries.
In the recent Phys. Rev. Lett. 135, 126503 (2025), F. Alet and S. Capponi and their collaborators have established the finite-temperature phase diagram of the quantum loop model on the triangular lattice, using large-scale quantum Monte-Carlo simulations. This collaboration was possible thanks to a joint ANR/RGC research grant between France and Hong Kong