
Alexander Mirlin (KIT)
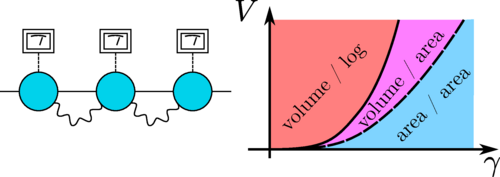
We study, both analytically and numerically, a problem of many-body fermionic system in d dimensions subjected to random measurements of local particle numbers. For free fermions, we develop an analytical approach based on the Keldysh path-integral formalism and replica trick, and derive a non-linear sigma model (NLSM) in d+1 dimensions as an effective field theory [1]. This establishes a close relation between measurement-induced phase transitions (MIPTs) and Anderson transitions, albeit with unconventional symmetry class and replica limits. On the Gaussian level, the NLSM predicts diffusive behavior, implying that the entanglement entropy grows with system size as logarithm times area. However, the renormalization-group analysis shows that, for d=1, the « weak localization of information » develops asymptotically into strong localization, implying that the system is in the area-law phase even for a small measurement rate [1]. The corresponding localization length is however exponentially large for rare measurements. For d>1, we obtain a MIPT between the « diffusive » and « localized » phases of information and charge correlations [2] and determine the critical exponent of the correlation (localization) length. Our key observables are the two-point density correlation function C(r) and the charge covariance between separated regions, G_{AB}, which are counterparts of two-point and two-terminal conductances, respectively. We further explore their fluctuations over the ensemble of quantum trajectories in the delocalized and localized phases, as well as at the transition point, thus laying the groundwork for mesoscopic theory of monitored systems [3]. The « metallic » phase is characterized by « universal conductance fluctuations » of G_{AB} and the critical point by scale-invariant distribution of G_{AB} and by multifractality of C(r). Including interaction between fermions induce additional terms in the NLSM that strongly affect the physics [4]. First, this leads to the “information-charge separation”: charge cumulants get decoupled from entanglement entropies. Second, the interaction stabilizes the volume-law phase for the entanglement. Third, for spatial dimensionality d=1, the interaction stabilizes the phase with logarithmic growth of charge cumulants.
If the time permits, I will also briefly discuss the emergence of Levy flights of quantum
information in monitored systems [5].
[1] I. Poboiko, P. Pöpperl, I.V. Gornyi, A.D. Mirlin, Phys. Rev. X 13, 041046 (2023)
[2] I. Poboiko, I.V. Gornyi, A.D. Mirlin, Phys. Rev. Lett. 132, 110403 (2024)
[3] I. Poboiko, I.V. Gornyi, A.D. Mirlin, arXiv: 2507.11312
[4] I. Poboiko, P. Pöpperl, I.V. Gornyi, A.D. Mirlin, Phys. Rev. B 111, 024204 (2025)
[5] I. Poboiko, M. Szyniszewski, C.J. Turner, I.V. Gornyi, A.D. Mirlin, A. Pal, arXiv:2501.12903
Contact : N. Laflorencie