PROLHAC Sylvain

Adresse : Laboratoire de Physique Théorique,
Université de Toulouse, 118 Route de Narbonne,
31062 Toulouse Cedex 4, France

Sujet de stage de Master 2
Proposition de thèse

Mes travaux portent sur une classe d’universalité hors d’équilibre en une dimension, connue sous le nom de KPZ, qui décrit les fluctuations de certaines interfaces en croissance ainsi que celles de fluides classiques et quantiques.

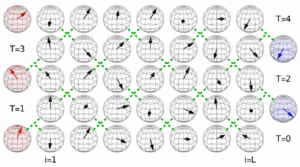
Je m’intéresse plus particulièrement à des effets de volume fini, correspondant à un régime pour lequel la longueur de corrélation des fluctuations est de l’ordre de grandeur de la taille du système. L’évolution temporelle du système décrit alors tout le processus de relaxation des fluctuations vers l’état stationnaire, partant d’un état initial donné.

En particulier, j’ai montré récemment que les fluctuations KPZ en volume fini décrivent le processus de relaxation vers l’état stationnaire dans certaines chaînes de spin intégrables :

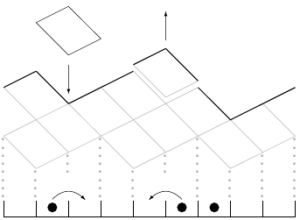
Sur la plan technique, les fluctuations KPZ en volume fini peuvent être obtenues en prenant la limite de grande échelle de systèmes de particules en interaction comme le modèle d’exclusion totalement asymétrique (TASEP) :

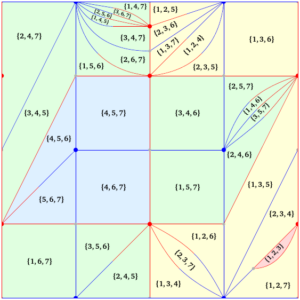
Des formules exactes font alors intervenir des intégrales de contour sur une surface de Riemann, dont le genre tend vers l’infini dans la limite KPZ :

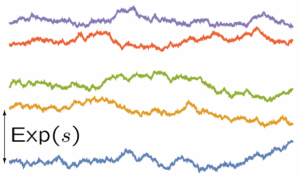
De plus, les fluctuations KPZ stationnaires possèdent une représentation simple en terme de processus browniens conditionnés à ne pas se croiser :

Sélection d’articles récents (liste complète sur arXiv) :

Article de revue, basé sur mon HDR :

• S.Prolhac, KPZ fluctuations in finite volume, SciPost Phys. Lect. Notes 81 (2024) (arXiv:2401.15016)

Formules exactes pour les fluctuations KPZ en volume fini

• S. Prolhac, Finite-time fluctuations for the totally asymmetric exclusion process, Phys. Rev. Lett. 116 (2016) 090601 (arXiv:1511.04064)

Application aux chaînes de spin intégrables

• S. Prolhac, Cheaper access to universal fluctuations in integrable spin chains from boundary effects (2025) (arXiv:2509.05176)

Processus browniens sans intersection

• S. Prolhac and K. Mallick, Brownian bridges for late time asymptotics of KPZ fluctuations in finite volume, J. Stat. Phys. 173 (2018) 322-361 (arXiv:1805.03187)
• S. Prolhac, Approach to stationarity for the KPZ fixed point with boundaries, EPL148 11002 (2024) (arXiv:2407.07012)

Surfaces de Riemann

• S. Prolhac, Riemann surfaces for KPZ with periodic boundaries, SciPost Phys. 8, 008 (2020) (arXiv:1908.08907)
• S. Prolhac, Riemann surface for TASEP with periodic boundaries, J. Phys. A: Math. Theor. 53 445003 (2020) (arXiv:2006.15096)
• S. Prolhac, Probability of a single current, J. Stat. Phys. 191 133 (2024) (arXiv:2308.11693)

Systèmes à plusieurs espèces de particules

• S. Prolhac, M. R. Evans and K. Mallick, Matrix product solution of the multispecies partially asymmetric exclusion process, J. Phys. A: Math. Theor. 42 165004 (2009) (arXiv:0812.3293)
• S. Prolhac, Current fluctuations for the second class particle : joint statistics, J. Phys. A: Math. Theor. 58 325004 (2025) (arXiv:2503.10531)

Trou spectral

• S. Prolhac, Perturbative solution for the spectral gap of the weakly asymmetric exclusion process, J. Phys. A: Math. Theor. (2017) 50:315001 (arXiv:1703.04596)
• U. Godreau and S. Prolhac, Spectral gaps of open TASEP in the maximal current phase, J. Phys. A: Math. Theor. (2020) 53 385006 (arXiv:2005.04461)